Câu hỏi/bài tập:
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm

Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Advertisements (Quảng cáo)

Hàm số trên xác định trên R
Ta có: \(y’ = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y’ = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
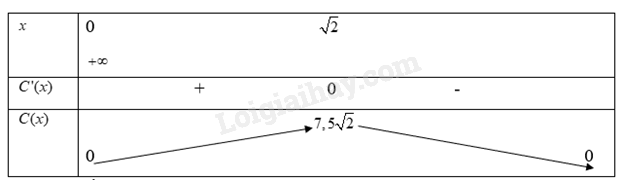
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút
