Bài 2. Cho khối lập phương \(ABCD.A’B’C’D’\) cạnh bằng \(a\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(B’C’\) và \(C’D’\). Mặt phẳng \((AEF)\) chia khối lập phương đó thành hai khối đa diện (H) và (H’) trong đó (H) là khối đa diện chứa đỉnh \(A’\). Tính thể tích của (H).

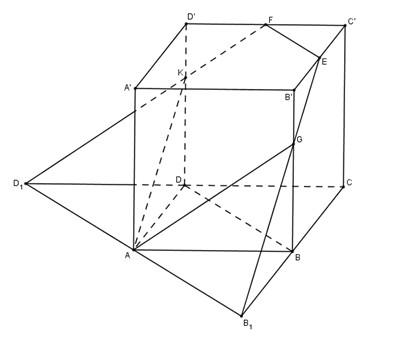
Cách vẽ thiết diện:
Ta có \(EF // B’D’\) mà \(B’D’ // BD\) nên từ \(A\) kẻ đường song song với \(BD\), cắt \(CD\) kéo dài tại \(D_1\) và \(CB\) kéo dài tại \(B_1\).
Nối \(B_1E\) cắt \(BB’\) tại \(G\). Nối \(D_1F\) cắt \(DD’\) tại \(K\).
Thiết diện là ngũ giác \(AGEFK\).
Hình (H) là khối \(AGEFK.A’B’D’\).
Theo giả thiết \(E\) là trung điểm của \(B’C’\); \(F\) là trung điểm của \(C’D’\), ta có
\(BB_1= BC = a = 2B’E\) \( \Rightarrow BG = 2GB’ = {2 \over 3}a\)
Từ đó \({V_{(A.B{B_1}G)}} = {1 \over 3}{S_{\Delta B{B_1}G}}.AB = {1 \over 9}{a^3} = {V_1}\)
Advertisements (Quảng cáo)
\({V_{(A.D{D_1}K)}} = {1 \over 3}.{S_{\Delta D{D_1}K}}.AD = {1 \over 9}{a^3} = {V_2}\)
Ta có \({S_{\Delta C{B_1}{D_1}}} = {1 \over 2}C{B_1}.C{D_1} = 2{a^2}\);
\({S_{\Delta EC’F}} = {1 \over 2}.C’E.C’F = {{{a^2}} \over 8}\)
Chiều cao hình chóp cụt \(CB_1D_1.C’EF \)là \(CC’ = a\)
\({V_{C{C_1}{D_1}.C’EF}} = {1 \over 3}a\left( {2{a^2} + {{{a^2}} \over 8} + {{{a^2}} \over 2}} \right) = {{7{a^3}} \over 8}\)
Thể tích của khối (H’) bằng:
\({V_{(H’)}} = {V_{C{C_1}{D_1}.C’EF}} - ({V_1} + {V_2}) = {7 \over 8}{a^3} - {2 \over 9}{a^3} \)
\(= {{47} \over {72}}{a^3}\)
Từ đó thể tích của khối (H) bằng:
\({V_{(H)}} = \)\(V\)lập phương - \(V\)(H’) = a3 - \({{47} \over {72}}{a^3} = {{25} \over {72}}{a^3}\)
