Bài 3. Cho mặt cầu \((S)\) tâm \(O\) bán kính \(r\). Hình nón có đường tròn đáy \((C)\) và đỉnh \(I\) đều thuộc \((S)\) được gọi là hình nón nội tiếp mặt cầu \((S)\). Gọi \(h\) là chiều cao của hình nón đó.
a) Tính thể tích của hình nón theo \(r\) và \(h\).
b) Xác định \(h\) để thể tích của hình nón là lớn nhất.

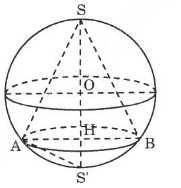
a) Cắt hình vẽ bằng một mặt phẳng qua trục hình nón, ta có hình vẽ trên, trong đó \(AH\) là bán kính đáy hình nón, \(SH\) là chiều cao hình nón \(SH = h\), \(SS’\) là đường kính hình cầu \(SS’ = 2r\).
Tam giác \(SAS’\) vuông tại đỉnh \(A\), và \(AH\) là đường cao nên:
\(AH^2= SH.S’H\) \( \Rightarrow AH^2 = h(2r - h)\)
Advertisements (Quảng cáo)
\(V\)nón = \({1 \over 3}\pi .A{H^2}.SH \Rightarrow V\)nón = \({1 \over 3}\pi {h^2}(2r - h)\)
b) Ta có:
\(V\)nón max \( \Leftrightarrow \) \(2V\)nón = \({\pi \over 3}.{h^2}(4r - 2h)\) lớn nhất.
Ta có \(h^2(4r - 2h) = h.h.(4r - 2h)\)\( \le {\left( {{{h + h + 4r - 2h} \over 3}} \right)^3} = {\left( {{{4r} \over 3}} \right)^3}\)
Dấu bằng xảy ra thì \(V\)nón lớn nhất.
Khi đó \(h = 4r - 2h\) \( \Rightarrow h = {4 \over 3}r\)
và \(V\)nón max = \({\pi \over 6}{\left( {{{4r} \over 3}} \right)^3} = {{32} \over {81}}\pi {r^3}\)
