Bài 10. Giải các bài toán sau đây bằng phương pháp tọa độ.
Cho hình lập phương \(ABCD.A’B’C’D’\) cạnh bằng \(1\).
a) Chứng minh rằng hai mặt phẳng \((AB’D’)\) và \((BC’D)\) song song với nhau.
b) Tính khoảng cách giữa hai mặt phẳng nói trên.
Giải.
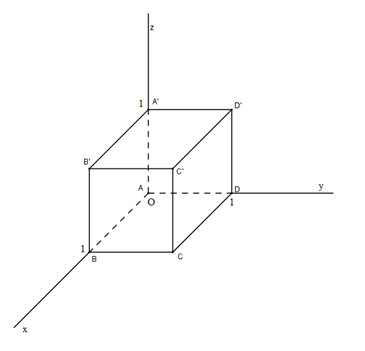
Xét hệ trục tọa độ \(Oxyz\) trong không gian sao cho \(A(0 ; 0 ; 0), B(1 ; 0 ; 0), D(0 ; 1 ; 0)\),\((A'(0 ; 0 ; 1)\). Khi đó \(B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C'(1 ; 1 ; 1)\).
a) Mặt phẳng \((AB’D’)\) qua điểm \(A\) và nhận vevtơ \(\overrightarrow{n}=\left [\overrightarrow{AB’},\overrightarrow{AD’} \right ]\) làm vectơ pháp tuyến. Ta có \(\overrightarrow{AB’} = (1 ; 0 ; 1)\), \(\overrightarrow{AD’} = (0 ; 1 ; 1)\) và \(\overrightarrow{n} = (-1 ; -1 ; 1)\).
Phương trình mặt phẳng \((AB’D’)\) có dạng:
\(x + y - z = 0\). (1)
Advertisements (Quảng cáo)
Tương tự, mặt phẳng \((BC’D)\) qua điểm \(B\) nhận vectơ \(\overrightarrow{m}=\left [\overrightarrow{BD},\overrightarrow{BC’} \right ]\) làm vectơ pháp tuyến.
Ta có \(\overrightarrow{BD} = (-1 ; 1 ; 0)\), \(\overrightarrow{BC’} = (0 ; 1 ; 1)\) và \(\overrightarrow{m} = (1 ; 1 ; -1)\).
Phương trình mặt phẳng \((BC’D)\) có dạng:
\( x + y - z - 1 = 0\). (2)
So sánh hai phương trình (1) và (2), ta thấy hai mặt phẳng \((AB’D’)\) và \((BC’D)\) song song với nhau.
Chú ý : Bài này có thể làm không cần phương pháp tọa độ như sau:
Xét hai mặt phẳng \((AB’D’)\) và \((BC’D)\), ta có \(BD // B’D’\) vì \(BB’D’D\) là hình chữ nhật, \(AD’ // BC’\) vì \(ABC’D’\) là hình chữ nhật.
Do đó mặt phẳng \((AB’D’)\) có hai đường thẳng cắt nhau \(B’D’\) và \(AD’\) lần lượt song song với hai đường thẳng cắt nhau \(BD\) và \(BC’\) của mặt phẳng \((BC’D)\). Vì vậy \((AB’D’) // (BC’D)\)
b) Vì \((AB’D’) // (BC’D)\) nên khoảng cách từ \(A\) đến mặt phẳng \((BC’D)\) chính là khoảng cách giữa hai mặt phẳng. Ta có:
\(h=d(A,(BC’D))=\frac{|-1|}{\sqrt{3}}=\frac{\sqrt{3}}{3}\).
