Câu 1 trang 25 sgk hình học 12: Bài 3. Khái niệm về thể tích của khối đa diện. Tính thể tích khối tứ diện đều cạnh a.
Câu 1. Tính thể tích khối tứ diện đều cạnh \(a\).
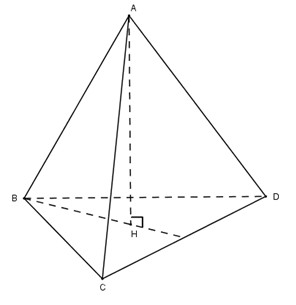
Cho tứ diện đều \(ABCD\). Hạ đường cao \(AH\) của tứ diện thì do các đường xiên \(AB, AC, AD\) bằng nhau nên các hình chiếu của chúng: \(HB, HC, HD\) bằng nhau. Do \(BCD\) là tam giác đều nên \(H\) là trọng tâm của tam giác \(BCD\).
Advertisements (Quảng cáo)
Do đó \(BH = {2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a\)
Từ đó suy ra: \(AH^2 \)=\( a^2\)– \(BH^2 \)=\({{6{a^2}} \over 9}\)
Nên \(AH = {{\sqrt 6 } \over 3}a\)
Thể tích tứ diện đó \(V={1 \over 3} \cdot {1 \over 2} \cdot {{\sqrt 3 } \over 2}{a^2} \cdot {{\sqrt 6 } \over 3}a = {a^3}{{\sqrt 2 } \over {12}}.\)