Câu 3 trang 25 sgk hình học 12: Bài 3. Khái niệm về thể tích của khối đa diện. Cho hình hộp ABCD.A’B’C’D’. Tính thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Câu 3. Cho hình hộp \(ABCD.A’B’C’D’\). Tính thể tích của khối hộp đó và thể tích của khối tứ diện \(ACB’D’\).
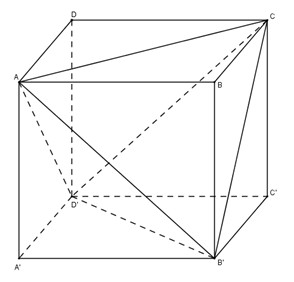
Gọi \(S\) là diện tích đáy \(ABCD\) và \(h\) là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện \(ACB’D’\) và bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\). Ta thấy bốn khối chóp sau đều có diện tích đáy bằng \(\frac{S}{2}\) và chiều cao bằng \(h\), nên tổng các thể tích của chúng bằng
Advertisements (Quảng cáo)
\(4\cdot \frac{1}{3}\cdot \frac{S}{2}h\)\(=\frac{2}{3}Sh\).
Từ đó suy ra thể tích của khối tứ diện
\(ACB’D’\)=\(\frac{1}{3}Sh\). Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện \(ACB’D’\) bằng \(3\).