Câu 2 trang 25 sgk hình học 12: Bài 3. Khái niệm về thể tích của khối đa diện. Tính thể tích khối bát diện đều cạnh a.
Câu 2. Tính thể tích khối bát diện đều cạnh \(a\).

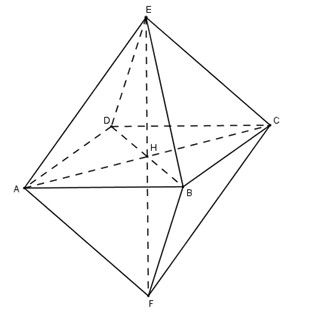
Chia khối tám mặt đều cạnh \(a\) thành hai khối chóp tứ giác đều cạnh \(a\).
Advertisements (Quảng cáo)
Gọi \(h\) là chiều cao của khối chóp thì dễ thấy
\({h^2} = {a^2} - {\left( {{a\sqrt {2}}\over2 } \right)^2} = {{{a^2}} \over 2}\) nên \(h = {{a\sqrt 2 } \over 2}\)
Từ đó thể tích khối tám mặt đều cạnh \(a\) là:
\(V = 2.{1 \over 3}.{{\sqrt {2}}\over2}a .{a^2} = {a^3}{{\sqrt 2 } \over 3}\).
