Câu 5. Cho tam giác \(ABC\) vuông cân ở \(A\) và \(AB = a\). Trên đường thẳng qua \(C\) và vuông góc với mặt phẳng \((ABC)\) lấy điểm \(D\) sao cho \(CD = a\). Mặt phẳng qua \(C\) vuông góc với \(SD\), cắt \(BD\) tại \(F\) và cắt \(AD\) tại \(E\). Tính thể tích khối tứ diện \(CDEF\) theo \(a\).

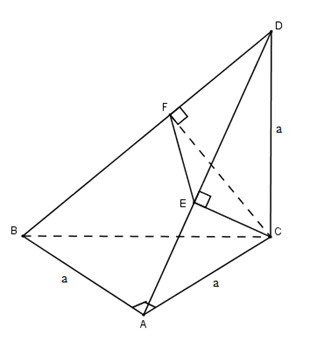
\(\left.\begin{matrix} BA \perp CD& \\ BA \perp CA& \end{matrix}\right\}\)\( \Rightarrow BA\bot (ADC)\) \(\Rightarrow BA \bot CE\)
Mặt khác \(BD \bot (CEF) \Rightarrow BD \bot CE\).
Từ đó suy ra
\(CE \bot (ABD) \Rightarrow CE ⊥ EF, CE \bot AD\).
Vì tam giác \(ACD\) vuông cân, \(AC= CD= a\) nên \(CE=\frac{AD}{2}=\frac{a\sqrt{2}}{2}\)
Advertisements (Quảng cáo)
Ta có \(BC = a\sqrt{2}\), \(BD = \sqrt{2a^{2}+a^{2}}=a\sqrt{3}\)
Để ý rằng \(CF\cdot BD = DC\cdot BC\) nên \(CF=\frac{a^{2}\sqrt{2}}{a\sqrt{3}}=a\sqrt{\frac{2}{3}}\)
Từ đó suy ra
\(EF= \sqrt{CF^{2}-CE^{2}}=\sqrt{\frac{2}{3}a^{2}-\frac{a^{2}}{2}}=\frac{\sqrt{6}}{6}a\).
\(DF=\sqrt{DC^{2}-CF^{2}}=\sqrt{a^{2}-\frac{2}{3}a^{2}}=\frac{\sqrt{3}}{3}a\).
Từ đó suy ra \(S_{\Delta CEF}=\frac{1}{2}FE\cdot EC=\frac{1}{2}\frac{a\sqrt{6}}{6}\cdot \frac{a\sqrt{2}}{2}=\frac{a^{2}\sqrt{3}}{12}\)
Vậy \(V_{D.CEF}=\frac{1}{3}S_{\Delta CEF}\cdot DF=\frac{1}{3}\cdot \frac{a^{2}\sqrt{3}}{12}\cdot \frac{a\sqrt{3}}{3}=\frac{a^{3}}{36}.\)
