
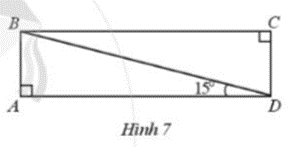
Ở Hình 7 có \(\widehat {BAD} = \widehat {BCD} = 90^\circ ,\widehat {ADB} = 15^\circ \) AD song song với BC. Chứng minh AB song song với DC.

Chứng minh: \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}\) suy ra AB // DC (hai góc so le trong bằng nhau)

Do AD // BC (giả thiết) nên \(\widehat {DBC} = \widehat {ADB} = 15^\circ \) (hai góc so le trong).
Advertisements (Quảng cáo)
Xét ∆BCD vuông tại C ta có:
\(\widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {BDC} = 90^\circ - \widehat {DBC} = 90^\circ - 15^\circ = 75^\circ \)
Xét ∆ABD vuông tại A ta có:
\(\widehat {AB{\rm{D}}} + \widehat {{\rm{AD}}B} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {AB{\rm{D}}} = 90^\circ - \widehat {A{\rm{D}}B} = 90^\circ - 15^\circ = 75^\circ \).
Do đó \(\widehat {ABD} = \widehat {BDC}\) (cùng bằng 75°)
Mà \(\widehat {AB{\rm{D}}}\) và \(\widehat {DBC}\) ở vị trí so le trong nên AB // DC.
Vậy AB // DC.
