
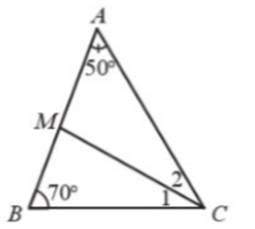
Cho tam giác ABC có Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo của \(\widehat {AMC}\) và \(\widehat {BMC}\)

- Tính góc C
- Vì CM là tia phân giác của góc C nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2}\)
- Tính số đo góc \(\widehat {AMC}\) và \(\widehat {BMC}\) dựa vào tổng ba góc trong một tam giác bằng \({180^o}\)

Advertisements (Quảng cáo)
Xét ∆ABC có: \(\widehat {{A^{}}} + \widehat B + \widehat C = {180^o}\) (định lí tổng ba góc của một tam giác).
Suy ra \(\widehat {ACB} = {180^o} - \widehat {{A^{}}} - \widehat B = {180^o} - {50^o} - {70^o} = {60^o}\)
Vì tia CM là tia phân giác của nên ta có:
\(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\)
Xét ∆AMC có: \(\widehat {AMC} + \widehat {{C_2}} + \widehat {{A^{}}} = {180^o}\) (tổng ba góc của một tam giác).
Suy ra \(\widehat {AMC} = {180^o} - \widehat {{C_2}} - \widehat {{A^{}}} = {180^o} - {30^o} - {50^o} = {100^o}\)
Xét ∆BMC có: \(\widehat {BMC} + \widehat {{C_1}} + \widehat B = {180^o}\) (tổng ba góc của một tam giác).
Suy ra \(\widehat {BMC} = {180^o} - \widehat {{C_1}} - \widehat B = {180^o} - {30^o} - {70^o} = {80^o}\)
Vậy \(\widehat {AMC} = {100^o};\widehat {BMC} = {80^o}\)
