
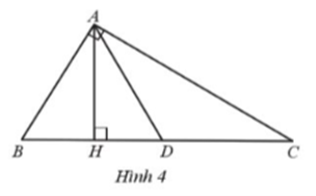
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H, AD là tia phân giác của \(\widehat {HAC}\) (hình 4)
a) Tìm các cặp góc có tổng số đo bằng 90°.
b) Cho \(\hat C = 40^\circ \). Tính số đo các góc \(\hat B,\widehat {BDA},\widehat {DAC}.\)
c) Chứng minh: \(\widehat {BAH} = \hat C,\widehat {CAH} = \hat B,\widehat {BAD} = \widehat {BDA}.\)

- Quan sát hình và sử dụng tổng hai góc nhọn của tam giác vuông bằng 90° để kể tên các cặp góc có tổng số đo bằng 90°.
- Sử dụng tổng ba góc trong một tam giác bằng \({180^o}\) và tia phân giác của một góc để tính số đo các góc \(\hat B,\widehat {BDA},\widehat {DAC}.\)
- Chứng minh: \(\widehat {BAH} = \widehat C = {90^o} - \widehat B;\widehat {CAH} = \widehat B = {90^o} - \widehat C\) và sử dụng \(\widehat {DAC} = \widehat {DAH}\) suy ra \(\widehat {BA{\rm{D}}} = \widehat {B{\rm{D}}A}\)

a) Xét ∆ABC vuông tại A ta có:
\(\hat B + \hat C = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ∆ABH vuông tại H ta có:
\(\hat B + \widehat {BAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ∆ACH vuông tại H ta có:
\(\hat C + \widehat {CAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ∆ADH vuông tại H ta có:
Advertisements (Quảng cáo)
\(\widehat {A{\rm{D}}H} + \widehat {DAH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Ta có: \(\widehat {BAC} = 90^\circ = \widehat {BAH} + \widehat {HAC} = \widehat {BAD} + \widehat {DAC}\)
Vậy các cặp góc có tổng số đo bằng 90° là:
\(\widehat {BAH}\) và \(\widehat {CAH}\); \(\widehat B\) và \(\widehat C\) ; \(\widehat B\) và \(\widehat {BAH}\); \(\widehat C\) và \(\widehat {CAH}\); \(\widehat {BA{\rm{D}}}\) và \(\widehat {DAC}\); \(\widehat {HA{\rm{D}}}\) và \(\widehat {A{\rm{D}}H}\).
b) • Do \(\hat B + \hat C = 90^\circ \) (chứng minh câu a) nên \(\hat B = 90^\circ - \hat C\)
Mà \(\hat C = 40^\circ \) nên \(\hat B = 90^\circ - 40^\circ = 50^\circ \).
• Do \(\hat C + \widehat {CAH} = 90^\circ \)(chứng minh câu a)
Nên \(\widehat {CAH} = 90^\circ - \hat C = 90^\circ - 40^\circ = 50^\circ \)
Mà AD là tia phân giác của \(\widehat {CAH}\) (giả thiết)
Do đó \(\widehat {DAC} = \widehat {DAH} = \frac{{\widehat {CAH}}}{2} = \frac{{50^\circ }}{2} = 25^\circ \)
• Do \(\widehat {A{\rm{D}}H} + \widehat {DAH} = {90^o}\) chứng minh câu a)
Nên \(\widehat {ADH} = 90^\circ - \widehat {DAH} = 90^\circ - 25^\circ = 65^\circ \) hay \(\widehat {BDA} = 65^\circ .\)
Vậy \(\hat B = 50^\circ ,\widehat {BDA} = 65^\circ ,\widehat {DAC} = 25^\circ .\)
c) Vì \(\hat B + \widehat {BAH} = 90^\circ \) (chứng minh câu a)
Nên \(\widehat {BAH} = 90^\circ - \hat B = 90^\circ - 50^\circ = 40^\circ \).
Khi đó \(\hat B = \widehat {CAH}\left( { = 50^\circ } \right)\).
Lại có \(\widehat {BAD} + \widehat {DAC} = 90^\circ ;\widehat {A{\rm{D}}H} + \widehat {DAH} = 90^\circ \) (chứng minh câu a)
Mà \(\widehat {DAC} = \widehat {DAH}\)suy ra \(\widehat {BAD} = \widehat {ADH}\) hay \(\widehat {BAD} = \widehat {BDA}.\)
Vậy \(\widehat {BAH} = \hat C,\widehat {CAH} = \hat B,\widehat {BAD} = \widehat {BDA}.\)
