
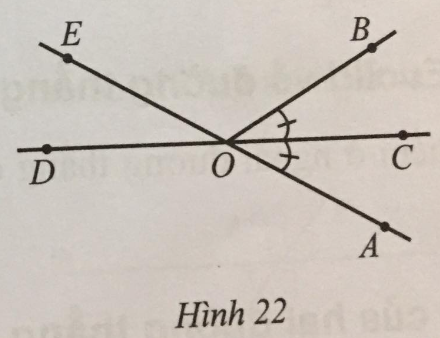
Ở Hình 22 có \(\widehat {AOB} = 60^\circ \), tia OC là tia phân giác của góc AOB.
a) Tính số đo mỗi góc BOC, BOE, COE, AOD.
b) Hai góc AOD và BOD có bằng nhau hay không?

a) Tính số đo mỗi góc dựa vào tia phân giác OC và hai góc đối đỉnh.
Advertisements (Quảng cáo)
b) Muốn biết hai góc có bằng nhau hay không, ta so sánh số đo của hai góc với nhau.

a) Do OC là tia phân giác của góc AOB nên \(\widehat {BOC} = \widehat {AOC} = \dfrac{1}{2}\widehat {AOB} = \dfrac{1}{2}{\rm{ }}.{\rm{ }}60^\circ = 30^\circ \).
Ta có: \(\widehat {BOE} + \widehat {AOB} = 180^\circ ,\widehat {COE} + \widehat {AOC} = 180^\circ ,\widehat {AOC} + \widehat {AOD} = 180^\circ \). (các cặp góc kề bù) nên
\(\begin{array}{l}\widehat {BOE} = 180^\circ - \widehat {AOB} = 180^\circ - 60^\circ = 120^\circ \\\widehat {COE} = \widehat {AOD} = 180 - \widehat {AOC} = 180^\circ - 30^\circ = 150^\circ \end{array}\)
b) Ta có: \(\widehat {BOD} + \widehat {BOC} = 180^\circ \to \widehat {BOD} = 180^\circ - \widehat {BOC} = 180^\circ - 30^\circ = 150^\circ \).
Do đó: \(\widehat {AOD} = \widehat {BOD} = 150^\circ \).
