Câu 103 trang 152 SBT Toán 7 tập 1: Chứng minh rằng CD là đường trung trực của...

Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh rằng CD là đường trung trực của AB.

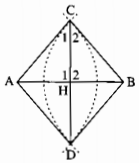
Gọi H là giao điểm của AB và CD

Nối AC, AD, BC, BD

Xét ∆ACD và ∆BCD, ta có:

AC = BC (bán kính hai cung tròn bằng nhau)

AD = BD (bán kính hai cung tròn bằng nhau)

CD cạnh chung

Suy ra ∆ACD = ∆BCD (c.c.c)

Suy ra: $\widehat {{C_1}} = \widehat {{C_2}}$ (hai góc tương ứng)

Xét hai tam giác AHC và BHC, ta có:

                 AC = BC (bán kính hai cung tròn bằng nhau)

                 $\widehat {{C_1}} = \widehat {{C_2}}$ (chứng minh trên)

                 CH cạnh chung

Suy ra: ∆AHC = ∆BHC (c.g.c)

Suy ra: AH = BH (hai cạnh tương ứng)                   (1)

Ta có: $\widehat {{H_1}} = \widehat {{H_2}}$ (hai cạnh tương ứng)

             $\widehat {{H_1}} + \widehat {{H_2}} = 180^\circ$ (hai góc kề bù)

Suy ra: $\widehat {{H_1}} = \widehat {{H_2}} = 90^\circ  \Rightarrow C{\rm{D}} \bot AB$                          (2)

Từ (1) và (2) suy ra CD là đường trung trực của AB.