Tìm các tam giác cân trên hình dưới.
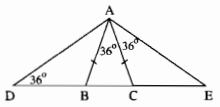

Ta có: AB = AC (gt) nên ∆ABC cân tại A.
\(\Rightarrow \widehat {ABC} = \widehat {ACB} = {{180^\circ - \widehat {BAC}} \over 2} = {{180^\circ - 36^\circ } \over 2} = 72^\circ \)
\(\widehat {BA{\rm{E}}} = \widehat {BAC} + \widehat {CA{\rm{E}}} = 36^\circ + 36^\circ = 72^\circ \)
\(\Rightarrow \widehat {BA{\rm{E}}} = \widehat {ABE}\) => ∆ABE cân tại E
\(\widehat E = 180^\circ - 2\widehat {ABE} = 180^\circ - 2.72^\circ = 36^\circ \)
Advertisements (Quảng cáo)
\(\widehat {CA{\rm{E}}} = \widehat E\) nên ∆ACE cân tại C.
Trong ∆DAC, ta có:
\(\widehat {DAC} = 180^\circ - \left( {\widehat D + \widehat {AC{\rm{D}}}} \right) = 180^\circ - \left( {36^\circ + 72^\circ } \right) = 72^\circ \)
Vì \(\widehat {DAC} = \widehat {AC{\rm{D}}}\) nên ∆DAC cân tại D
\(\eqalign{
& \widehat {DAC} = \widehat {DAB} + \widehat {BAC} \cr
& \Rightarrow \widehat {DAB} = \widehat {DAC} - \widehat {BAC} = 72^\circ - 36^\circ = 36^\circ \cr} \)
\( \Rightarrow \widehat {DAB} = \widehat D\) nên ∆ABD cân tại B
\(\widehat {A{\rm{D}}E} = \widehat {A{\rm{ED}}} = 36^\circ \) nên ∆ADE cân tại A
Vậy có 6 tam giác cân trong hình trên.
