Cho tam giác ABC có \(\widehat A = 60^\circ ,\widehat C = 50^\circ \). Tia phân giác của góc B cắt AC ở D. Tính \(\widehat {ADB},\widehat {CDB}\).

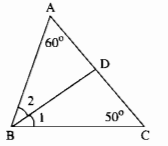
Trong ∆ABC ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
\(\eqalign{
& \Rightarrow \widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) \cr
& \Rightarrow x = 180^\circ - \left( {60^\circ + 50^\circ } \right) = 70^\circ \cr} \)
\(\widehat {{B_1}} = \widehat {{B_2}} = {1 \over 2}\widehat B\) (Vì BD là tia phân giác)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = 70^\circ :2 = 35^\circ \)
Trong ∆BDC ta có \(\widehat {A{\rm{D}}B}\) là góc ngoài tại đỉnh D.
\( \Rightarrow \widehat {A{\rm{D}}B} = \widehat {{B_1}} + \widehat C\) (tính chất góc ngoài tam giác)
\( \Rightarrow \widehat {A{\rm{D}}B} = 35^\circ + 50^\circ = 85^\circ \)
\(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {B{\rm{D}}C} = 180^\circ - \widehat {A{\rm{D}}B} = 180^\circ - 85^\circ = 95^\circ \)
