Chứng minh rằng MN // BC.. Câu 68 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 6: Tam giác cân
Cho tam giác ABC cân tại A có \(\widehat A = 100^\circ\). Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC.
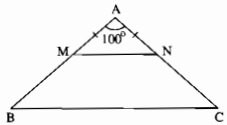
Vì ∆ABC cân tại A nên \(\widehat B = \widehat C\)
Ta có: \(\widehat B = {{180^\circ - \widehat A} \over 2}\)
Advertisements (Quảng cáo)
\( = {{180^\circ - 100^\circ } \over 2} = 40^\circ \) (1)
Mà AM = AN (gt) nên ∆AMN cân tại A => \(\widehat {AMN} = \widehat {ANM}\)
\(\Rightarrow \widehat {AMN} = {{180^\circ - \widehat A} \over 2} = {{180^\circ - 100^\circ } \over 2} = 40^\circ \) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat {AMN}\)
Vậy MN // BC (vì có cặp góc ở vị trí đồng vị bằng nhau).