Chứng minh rằng ∆OBC là tam giác cân. Câu 70 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 6: Tam giác cân
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK . Gọi O là giao điểm của BH và CK. Chứng minh rằng ∆OBC là tam giác cân.
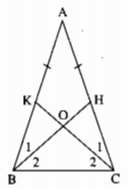
Xét ∆ABH và ∆ACK, ta có:
AB = AC (gt)
\(\widehat A\) chung
Advertisements (Quảng cáo)
AH = AK (gt)
Suy ra: ∆ABH = ∆ACK (c.g.c)
\(\Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\) (hai góc tương ứng)
\(\eqalign{
& \widehat {ABC} = \widehat {{B_1}} + \widehat {{B_2}}\left( 2 \right) \cr
& \widehat {ACB} = \widehat {{C_1}} + \widehat {{C_2}}\left( 3 \right) \cr} \)
\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân) (4)
Từ (1), (2), (3) và (4) suy ra: \(\widehat {{B_2}} = \widehat {{C_2}}\) hay ∆BOC cân tại O.