Cho hình bên.
a) Chứng minh rằng: \(CI \bot AB.\)
b) Cho \(\widehat {ACB} = 40^\circ \). Tính \(\widehat {BI{\rm{D}}},\widehat {DIE}\)

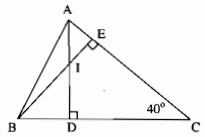
a) Trong ∆ABC ta có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của ∆ABC
\( \Rightarrow \) CI là đường cao thứ ba
Vậy \(CI \bot AB\)
b) Trong tam giác vuông BEC có
Advertisements (Quảng cáo)
\(\widehat {BEC} = 90^\circ \)
\( \Rightarrow \widehat {EBC} + \widehat C = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {EBC} = 90^\circ - \widehat C = 90^\circ - 40^\circ = 50^\circ \) hay \(\widehat {IB{\rm{D}}} = 50^\circ \)
Trong tam giác IDB có \(\widehat {I{\rm{DB}}} = 90^\circ \)
\( \Rightarrow \widehat {IB{\rm{D}}} + \widehat {BI{\rm{D}}} = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {BI{\rm{D}}} = 90^\circ - \widehat {IB{\rm{D}}} = 90^\circ - 50^\circ = 40^\circ \)
\(\widehat {BI{\rm{D}}} + \widehat {DIE} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {DIE} = 180^\circ - \widehat {BI{\rm{D}}} = 180^\circ - 40^\circ = 140^\circ \)
