Câu hỏi Bài 9 trang 82 Toán 7 Tập 2 :  ...

Hãy phát biểu và chứng minh các trường hợp còn lại của nhận xét trên (xem như những bài tập).

Áp dụng: Tính chất của các đường trung trực, phân giác, trung tuyến, đường cao.

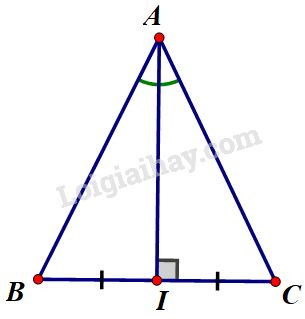
- Bài tập 1: Nếu một tam giác có một đường trung trực đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

Xét $ΔABC$ có $AI$ vừa là đường trung trực vừa là đường phân giác

$AI$ là đường trung trực của $BC$ $\Rightarrow$ $AB = AC$ (Tính chất đường trung trực đoạn thẳng)

$\Rightarrow  ΔABC$ cân tại $A$.

- Bài tập 2: Nếu một tam giác có một đường trung trực đồng thời là đường cao thì tam giác đó là một tam giác cân.

Xét $ΔABC$ có $AI$ vừa là đường trung trực vừa là đường cao.

$AI$ là đường trung trực của $BC$ $\Rightarrow$ $AB = AC$ (Tính chất đường trung trực đoạn thẳng)

$\Rightarrow  ΔABC$ cân tại $A$.

- Bài tập 3: Nếu một tam giác có một đường phân giác đồng thời là đường cao thì tam giác đó là một tam giác cân.

Xét $ΔABC$ có $AI$ vừa là đường phân giác vừa là đường cao

$AI$ là đường cao $\Rightarrow  AI ⊥ BC$

Xét hai tam giác vuông $ΔABI$ và $ΔACI$ có:

+) $AI$ chung

+) $\widehat {BAI} = \widehat {CAI}$ (do $AI$ là phân giác góc $BAC$)

$\Rightarrow  ΔABI = ΔACI$ (góc nhọn – cạnh góc vuông)

$\Rightarrow  AB = AC$(hai cạnh tương ứng)

$\Rightarrow  ΔABC$ cân tại $A$.

- Bài tập 4: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là một tam giác cân.

Xét $ΔABC$ có $AI$ vừa là đường trung tuyến vừa là đường cao

$AI$ là đường cao suy ra $AI ⊥ BC$.

$AI$ là đường trung tuyến $\Rightarrow$ $I$ là trung điểm $BC$.

Do đó $AI$ là đường trung trực của $BC$

$\Rightarrow  AB = AC$ (Tính chất đường trung trực của đoạn thẳng)

$\Rightarrow  ΔABC$ cân tại $A$.