Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ các đường thẳng song song với các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E. Tính tổng DE + DF.

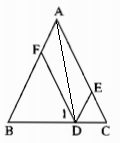
Ta có: DF // AC (gt)
\( \Rightarrow \widehat {{D_1}} = \widehat C\) (hai góc đồng vị) (1)
Lại có: ∆ABC cân tại A
\( \Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat {{D_1}}\)
Advertisements (Quảng cáo)
Hay ∆BFD cân tại F => BF = DF
Nối AD. Xét ∆AFD và ∆DEA, ta có:
\(\widehat {A{\rm{D}}F} = \widehat {E{\rm{AD}}}\) (so le trong vì DF // AC)
AD cạnh chung
\(\widehat {F{\rm{D}}A} = \widehat {E{\rm{D}}A}\) (so le trong vì DE // AB)
Suy ra: ∆ADF = ∆DAE (g.c.g) => AF = DF (hai cạnh tương ứng)
Vậy: DE + DF = AF + BF = AB = 3(cm)
