Tính số đo góc BCD.. Câu 75 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 6: Tam giác cân
Cho tam giác ABC cân tạiA) Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD
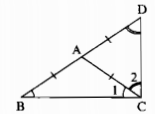
Ta có: ∆ABC cân tại A
\( \Rightarrow \widehat B = \widehat {{C_1}}\) (tính chất tam giác cân)
Lại có: AD = AB (gt)
=>AD = AC do đó ∆ACD cân tại A
Advertisements (Quảng cáo)
\( \Rightarrow \widehat D = \widehat {{C_2}}\) (tính chất tam giác cân)
Mà \(\widehat {BC{\rm{D}}} = \widehat {{C_1}} + \widehat {{C_2}}\)
Nên \(\widehat {BC{\rm{D}}} = \widehat B + \widehat D\) (1)
Trong ∆BCD, ta có:
\(\widehat B + \widehat D + \widehat {BC{\rm{D}}} = 180^\circ \) (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: \(2\widehat {BC{\rm{D}}} = 180^\circ \) hay \(\widehat {BC{\rm{D}}} = 90^\circ \)