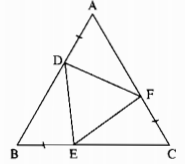
Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh rằng ∆DEF là tam giác đều.

Ta có: AB = AD + DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC (gt) (4)
AD = BE = CF (gt) (5)
Từ (1), (2), (3), (4) và (5) suy ra:
BD = EC = AF
Xét ∆ADF và ∆BED, ta có:
AD = BE (gt)
Advertisements (Quảng cáo)
\(\widehat A = \widehat B = 60^\circ \) (vì ∆ABC đều)
AE = BD (chứng minh trên)
Suy ra: ∆ADF = ∆BED (c.g.c)
Suy ra: DF = DE (hai cạnh tương ứng) (6)
Xét ∆ADF và ∆CFE ta có:
AD = CF (gt)
\(\widehat A = \widehat C = 60^\circ \) (vì ∆ABC đều)
EC = AF (chứng minh trên)
Suy ra : ∆ADF = ∆CFE (c.g.c)
Suy ra: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy ∆DEF đều.
