Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D, E. Chứng minh rằng DE = BD + CE

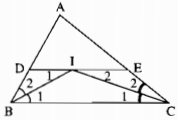
Ta có: DI // BC (gt)
\( \Rightarrow \widehat {{I_1}} = \widehat {{B_1}}\) (so le trong) (1)
Lại có: \({\widehat B_1} = \widehat {{B_2}}\) (2)
(vì BI là tia phân giác của \(\widehat B\))
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \(\widehat {{I_1}} = \widehat {{B_2}}\)
\( \Rightarrow \) ∆BDI cân tại D => BD = DI (3)
Mà IE // BC (gt) => \(\widehat {{I_2}} = \widehat {{C_1}}\) (so le trong) (4)
Đồng thời: \(\widehat {{C_1}} = \widehat {{C_2}}\) (Vì CI là tia phân giác của \(\widehat {{C_1}}\)) (5)
Từ (4) và (5) suy ra: \(\widehat {{I_2}} = \widehat {{C_2}}\) => ∆CEI cân tại E
\( \Rightarrow \) CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE.
