Chứng minh rằng BD vuông góc với AC.. Câu 78 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 9: Tính chất ba đường cao của tam giác
Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.

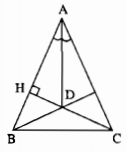
∆ABC cân tại A, đường phân giác của góc ở đỉnh cũng là đường cao.
Advertisements (Quảng cáo)
Do đó:
\(\eqalign{
& A{\rm{D}} \bot BC \cr
& CH \bot AB\left( {gt} \right) \cr} \)
Trong ∆ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC, do đó BD là đường cao xuất phát từ đỉnh B đến cạnh đối diện AC.
Vậy \(B{\rm{D}} \bot AC\).
