Chứng minh rằng góc AHB nhỏ hơn góc HAC.. Câu 80 trang 51 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 9: Tính chất ba đường cao của tam giác
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn, AC < AB. Kẻ đường cao AH. Chứng minh rằng \(\widehat {AHB} < \widehat {HAC}\).
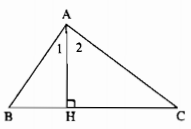
Trong ∆ABC ta có: AC > AB
\(\Rightarrow \widehat B > \widehat C\) (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat B + \widehat {{A_1}} = 90^\circ \) (tính chất tam giác vuông) (1)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\( \Rightarrow \widehat C + \widehat {{A_2}} = 90^\circ \) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat B + \widehat {{A_1}} = \widehat C + \widehat {{A_2}}\)
Mà \(\widehat B > \widehat C\) nên \(\widehat {{A_1}} < \widehat {{A_2}}\)