Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 62) là tam giác nhọn. Câu 81 trang 148 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 6: Tam giác cân
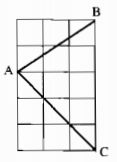
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 62) là tam giác nhọn.
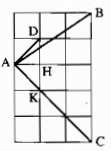
Nối A với điểm D tạo thành đường chéo ô vuông
Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ô vuông từ A.
Advertisements (Quảng cáo)
Ta có: ∆AHK vuông cân tại H => \(\widehat {HAK} = 45^\circ \)
∆AHD vuông cân tại H => \(\widehat {HA{\rm{D}}} = 45^\circ \)
\( \Rightarrow \widehat {DAK} = \widehat {HA{\rm{D}}} + \widehat {HAK} = 45^\circ + 45^\circ = 90^\circ \) hay \(\widehat {DAC} = 90^\circ \)
\( \Rightarrow \widehat {BAC} < 90^\circ \)
Trên hình vẽ: \(\widehat {ACB} < 90^\circ \) và \(\widehat {ABC} < 90^\circ \)
Vậy ∆ABC là tam giác nhọn.