
Cho tam giác ABC nhọn. Về phía ngoài tam giác ABC vẽ tam giác BAD vuông cân tại A, tam giác CAE vuông cân tại A. Chung minh rằng :
a) DC = BE.
b) \(DC \bot BE.\)
c) \(B{D^2} + C{E^2} = B{C^2} + D{E^2}.\)

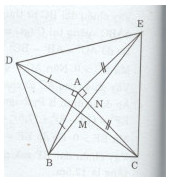
a)Ta có: \(\eqalign{ & \widehat {BAE} = \widehat {CAE} + \widehat {BAC} = {90^0} + \widehat {BAC} \cr & \widehat {DAC} = \widehat {DAB} + \widehat {BAC} = {90^0} + \widehat {BAC} \cr} \)
Nên \(\widehat {BAE} = \widehat {DAC}\)
Xét hai tam giác ADC và ABE có:
AD = AB (tam giác BAD vuông cân tại A)
\(\widehat {DAC} = \widehat {BAE},AC = AE(\Delta CAE\) vuông cân tại A)
Do đó: \(\Delta ADC = \Delta ABE(c.g.c) \Rightarrow CD = BE.\)
b) Gọi M, N lần lượt là giao điểm của BE với CD, AC.
Advertisements (Quảng cáo)
Ta có: \(\widehat {ANE} + \widehat {AEN} = {90^0}(\Delta ANE\) vuông tại A).
Mà \(\widehat {ANE} = \widehat {MNC}\) (đối đỉnh), \(\widehat {AEN} = \widehat {MCN}(\Delta ADC = \Delta ABE)\)
Suy ra \(\widehat {MNC} + \widehat {MCN} = \widehat {ANE} + \widehat {AEN} = {90^0}.\)
Tam giác CMN có: \(\widehat {NMC} + \widehat {MNC} + \widehat {MCN} = {180^0}\)
Do đó: \(\widehat {NMC} = {180^0} - {90^0} = {90^0}.\) Vậy \(CD \bot BE.\)
Tam giác MBD vuông tại M \(\Rightarrow B{D^2} = M{B^2} + M{D^2}\) (định lí Pythagore)
Tam giác MCE vuông tại M \(\Rightarrow C{E^2} = M{C^2} + M{E^2}\) (định lí Pythagore)
Do đó: \(B{D^2} + C{E^2} = M{B^2} + M{D^2} + M{C^2} + M{E^2}(1)\)
Tam giác MBC vuông tại M \(\Rightarrow B{C^2} = M{B^2} + M{C^2}\) (định lí Pythagore)
Tam giác MDE vuông tại M \(\Rightarrow D{E^2} = M{D^2} + M{E^2}\) (định lí Pythagore)
Do đó: \(B{C^2} + D{E^2} = M{B^2} + M{C^2} + M{D^2} + M{E^2}(2)\)
Tà (1) và (2) ta có: \(B{D^2} + C{E^2} = B{C^2} + D{E^2}\)
