
Cho tam giác ABC cân tại A. Kẻ \(BM \bot AC(M \in AC),CN \bot AB(N \in AB).\)
a) Chứng minh rằng \(\Delta BMC = \Delta CNB.\)
b) Gọi I là giao điểm của BM với CN. Chứng minh rằng \(\Delta AIN = \Delta AIM.\)
c) AI cắt BC tại H, biết AB = 10 cm, BC = 12 cm. Tính AH.

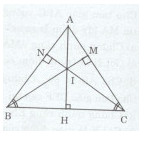
a)Xét tam giác BMC vuông tại M và CNB vuông tại N có:
BC là cạnh chung.
\(\widehat {MCB} = \widehat {NBC}\) (tam giác ABC cân tại A)
Do đó: \(\Delta BMC = \Delta CVB\) (cạnh huyền - góc nhọn)
b) Ta có: AN + NB = AB và AM + MC = AC.
Mà AB = AC (tam giác ABC cân tại A)
Nên AN + NB = AM + MC.
Vì BN = MC \((\Delta BMC = \Delta CNB)\)
Nên AN = AM.
Advertisements (Quảng cáo)
Xét tam giác ANI vuông tại N và AMI vuông tại M ta có:
AI là cạnh chung.
AN = AM (chứng minh trên)
Do đó: \(\Delta ANI = \Delta AMI\) (cạnh huyền - cạnh góc vuông).
c)Xét tam giác ABH và ACH ta có:
AB = AC (tam giác ACB cân tại A)
AH là cạnh chung.
\(\widehat {BAH} = \widehat {CAH}(\Delta ANI = \Delta AMI)\)
Do đó: \(\Delta ABH = \Delta ACH(c.g.c) \Rightarrow BH = CH;\widehat {AHB} = \widehat {AHC}\)
Do đó: \(BH = CH = {{BC} \over 2} = {{12} \over 2} = 6(cm).\)
\(\widehat {AHB} + \widehat {AHC} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {AHB} + \widehat {AHB} = {180^0}(\widehat {AHB} = \widehat {AHC}) \Rightarrow 2\widehat {AHB} = {180^0} \Rightarrow \widehat {AHB} = {90^0} \Rightarrow AH \bot BC\)
Tam giác ABH vuông tại H \(\Rightarrow A{H^2} + B{H^2} = A{B^2}\) (định lí Pythagore).
Do đó: \(A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2} = 100 - 36 = 64.\)
Mà AH > 0. Vậy \(AH = \sqrt {64} = 8(cm).\)
