
Vẽ trên cùng một hình:
a) Góc xOy có số đo bằng 60o
b) Góc x’Oy’ đối đỉnh với góc xOy.
c) Tia phân giác Ot của góc xOy.
d) Tia Ot’ là tia đối của tia Ot.
- Tia Ot’ có là tia phân giác của góc x’Oy’ không ?
- Viết tên 6 cặp góc đối đỉnh và tính số đo của mỗi góc đó.

a)b)c)
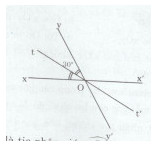
d) Ta có: \(\widehat {xOt} = \widehat {yOt}\) (Ot là tia phân giác góc xOy)
\(\widehat {xOt} = \widehat {x’Ot’}\) (đối đỉnh) và \(\widehat {yOt} = \widehat {y’Ot’}\) (đối đỉnh) \( \Rightarrow \widehat {x’Ot’} = \widehat {y’Ot’}\)
Mà tia Ot’ nằm giữa hai tia Ox’, Oy’. Vậy Ot’ là tia phân giác của góc xOy
Có 6 cặp góc đối đỉnh là:
Advertisements (Quảng cáo)
xOt và x’Ot’; yOt và y’Ot’; x’Oy và xOy’
xOy và x’Oy’; x’Ot và xOt’; y’Ot và yOt’.
Ta có: \(\widehat {xOt} = \widehat {yOt} = {1 \over 2}\widehat {xOy} = {30^0}\) (Ot là tia phân giác góc xOy)
\(\widehat {xOy} + \widehat {x’Oy} = {180^0}\) (kề bù)
Do đó: \(\widehat {x’Oy} = {180^0} - \widehat {xOy} = {180^0} - {60^0} = {120^0}\)
\(\widehat {yOt’} + \widehat {yOt} = {180^0}\) (kề bù) \( \Rightarrow \widehat {yOt’} = {180^0} - \widehat {yOt} = {180^0} - {30^0} = {150^0}\)
Và \(\widehat {x’Ot} + \widehat {xOt} = {180^0}\) (kề bù) \( \Rightarrow \widehat {x’Ot} = {180^0} - \widehat {xOt} = {180^0} - {30^0} = {150^0}\)
\(\widehat {x’Ot’} = \widehat {xOt} = {30^0}\) (hai góc đối đỉnh)
\(\widehat {y’Ot’} = \widehat {yOt} = {30^0}\)
\(\widehat {xOy’} = \widehat {x’Oy} = {120^0}\) (hai góc đối đỉnh)
\(\widehat {x’Oy’} = \widehat {xOy} = {60^0}\) (hai góc đối đỉnh)
\(\widehat {y’Ot} = \widehat {yOt’} = {150^0}\) (hai góc đối đỉnh)
\(\widehat {xOt’} = \widehat {x’Ot} = {150^0}\) (hai góc đối đỉnh)
