
Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
a) Vì sao cặp góc so le trong còn lại cũng bằng nhau ?
b) Vì sao các cặp góc đồng vị cũng bằng nhau ?
c) Vì sao các cặp góc trong cùng phía bù nhau ?

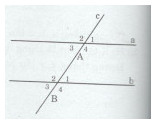
Đường thẳng c cắt hai đường thẳng a và b tạo thành hai góc A4 và B2 so le trong bằng nhau.
a)Ta có: \(\widehat {{A_4}} + \widehat {{A_3}} = \widehat {{B_1}} + \widehat {{B_2}}\)
(=1800 hai cặp góc kề bù)
Mà \(\widehat {{A_4}} = \widehat {{B_2}}\) (giả thiết) nên \(\widehat {{A_3}} = \widehat {{B_1}}\)
Vậy các cặp góc so le trong còn lại cũng bằng nhau.
Advertisements (Quảng cáo)
b) Ta có: \(\widehat {{A_3}} = \widehat {{B_1}}\) (chứng minh câu a) và \(\widehat {{A_1}} = \widehat {{A_3}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\)
\(\widehat {{A_3}} = \widehat {{B_1}}\) (chứng minh ở câu a) và \(\widehat {{B_2}} = \widehat {{B_3}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_3}} = \widehat {{B_3}}\)
Ta có: \(\widehat {{A_4}} = \widehat {{B_2}}\) (hai góc sole trong) và \(\widehat {{B_2}} = \widehat {{B_4}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_4}} = \widehat {{B_4}}\)
Ta có: \(\widehat {{A_4}} = \widehat {{B_2}}\) (hai góc sole trong) và \(\widehat {{A_2}} = \widehat {{A_4}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_2}} = \widehat {{B_2}}\)
Vậy các cặp góc đồng vị cũng bằng nhau.
c) Ta có: \(\widehat {{A_1}} + \widehat {{A_4}} = {180^0}\) (hai góc kề bù) và \(\widehat {{A_1}} = \widehat {{B_1}}\) (chứng minh câu b)
Suy ra: \(\widehat {{B_1}} + \widehat {{A_4}} = {180^0}\)
Ta có: \(\widehat {{A_2}} + \widehat {{A_3}} = {180^0}\) (hai góc kề bù) và \(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh câu b)
Suy ra: \(\widehat {{B_2}} + \widehat {{A_3}} = {180^0}\)
Vậy các cặp góc trong cùng phía bù nhau.
