
Trên đường thẳng xy lấy điểm O. Vẽ tia Ot sao cho góc xOt bằng 30o. Trên nửa mặt phẳng bờ xy không chứa Ot, vẽ tia Oz sao cho góc xOz bằng 120o. Chứng tỏ rằng góc xOt và góc yOz. Chứng tỏ rằng góc xOt và góc yOt’ là hai góc đối đỉnh.

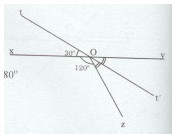
Ta có: \(\widehat {xOt} + \widehat {tOy} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {tOy} = {180^0} - {30^0} = {150^0}\)
\(\widehat {yOz} + \widehat {xOz} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {yOz} = {180^0} - {120^0} = {60^0}\)
\( \Rightarrow \widehat {yOt’} = \widehat {zOt’} = {{\widehat {yOz}} \over 2} = {{{{60}^0}} \over 2} = {30^0}\)
Advertisements (Quảng cáo)
(Ot’ là tia phân giác góc yOz)
Ta có: \(\widehat {tOy} + \widehat {yOt’} = {150^0} + {30^0} = {180^0} \Rightarrow \widehat {tOt’} = {180^0}\)
Do đó Ot là tia đối của tia Ot’.
Mặt khác Ox cũng là tia đối của tia Oy
Suy ra góc xOt và yOt’ là hai góc đối đỉnh.
