
Cho hình 52, biết \(FG = FH,\,\,\widehat G = \widehat H,\,\,FI\) là tia phân giác của \(\widehat {GFH}\)
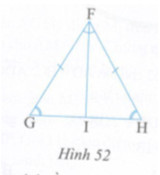
Chứng minh rằng:
\(\eqalign{ & a)\,\,\Delta FIG = \Delta FIH \cr & b)\,\,FI \bot GH \cr} \)

a)Xét tam giác FIG và FIH có:
\(\eqalign{ & \widehat {IGF} = \widehat {IHF}(gt) \cr & GF = HF \cr} \)
Advertisements (Quảng cáo)
\(\widehat {GFI} = \widehat {HFI}\) (Do FI là tia phân giác của góc GFH)
Do đó: \(\Delta FIG = \Delta FIH(g.c.g)\)
b) Tam giác GFH có: \(\widehat G + \widehat H + \widehat {GFH} = {180^0}\)
\( \Leftrightarrow \widehat G + \widehat G + 2\widehat {GFI} = {180^0}\) (Do \(\widehat H = \widehat G\) và FI là tia phân giác của góc GFH)
\( \Leftrightarrow 2\widehat G + 2\widehat {GFI} = {180^0} \Leftrightarrow \widehat G + \widehat {GFI} = {90^0}\)
Mà \(\widehat {FIH} = \widehat G + \widehat {GFI}\) (góc ngoài của tam giác GFI). Nên \(\widehat {FIH} = {90^0}.\) Do đó: \(FI \bot GH.\)
