
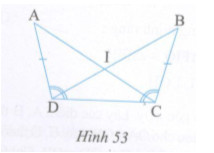
Ở hình 53 cho biết \(AD = BC,\,\,\widehat {ADC} = \widehat {BCD}.\) Chứng minh rằng:
\(\eqalign{ & a)\,\,\Delta ADC = \Delta BCD \cr & b)IA = IB \cr} \)

a)Xét tam giác ADC và BCD ta có:
AD = BC (gt)
\(\widehat {ADC} = \widehat {BCD}(gt)\)
Advertisements (Quảng cáo)
DC là cạnh chung.
Do đó: \(\Delta ADC = \Delta BCD(c.g.c)\)
b) Ta có:
\(\eqalign{ & *\Delta ADC = \Delta BCD \Rightarrow \widehat {DAC} = \widehat {CBD};\widehat {ACD} = \widehat {BDC} \cr & \widehat {ADI} + \widehat {IDC} = \widehat {ADC};\widehat {BCI} + \widehat {ICD} = \widehat {BCD} \cr} \)
Mà \(\widehat {ADC} = \widehat {BCD};\widehat {ACD} = \widehat {BDC}\) nên \(\widehat {ADI} = \widehat {BCI}\)
Xét tam giác ADI và BCI ta có: \(\eqalign{ & \widehat {ADI} = \widehat {BCI}(cmt) \cr & AD = BC(gt) \cr & \widehat {DAI} = \widehat {CBI}(\widehat {DAC} = \widehat {CBD}) \cr} \)
Do đó: \(\Delta ADI = \Delta BCI(g.c.g) \Rightarrow IA = IB.\)
