Luyện tập - Chủ đề 1: Góc tạo bởi các đường thẳng - Bài tập 8 trang 118 Tài liệu dạy – học Toán 7 tập 1. Giải bài tập Cho hình 20, biết
Cho hình 20, biết \(\widehat {{A_2}} = {140^o},\,\,\widehat {{B_1}} = {40^o}\) . Tính số đo các góc còn lại.
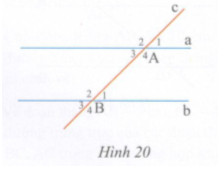
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = {180^0}\) (kề bù) nên \(\widehat {{A_1}} + {140^0} = {180^0}\)
\( \Rightarrow \widehat {{A_1}} = {180^0} - {140^0} = {40^0}\)
Advertisements (Quảng cáo)
Mặt khác \(\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\) (kề bù) nên \({40^0} + \widehat {{B_2}} = {180^0} \Rightarrow \widehat {{B_2}} = 180 - 40 = {140^0}\)
\(\widehat {{A_4}} = \widehat {{A_2}} = {140^0}\) (hai góc đối đỉnh)
\(\widehat {{B_3}} = \widehat {{B_1}} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {{A_3}} = \widehat {{A_1}} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {{B_4}} = \widehat {{B_2}} = {140^0}\) (hai góc đối đỉnh)