
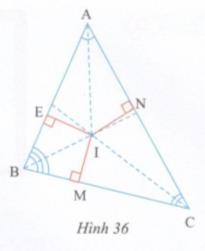
Dựa vào hình 36, hãy viết giả thiết, kết luận và chứng minh định lí theo gợi ý sau:
Gọi I là giao điểm của hai đường phân giác xuất phát từ đỉnh B và C của tam giác ABC, kẻ \(IM \bot BC,\,\,IE \bot AB,\,\,IN \bot AC\) (xem hình vẽ).
Hãy chứng minh:
* IM = IN = IE
* AI là tia phân giác của góc A.

Advertisements (Quảng cáo)

Chứng minh:
a) Ta có I nằm trên tia phân giác của \(\eqalign{ & \widehat {ABC}(gt),IE \bot AB(gt),IM \bot BC(gt) \cr & \Rightarrow IE = IM(1) \cr}\)
Ta cũng có I nằm trên tia phân giác của \(\eqalign{ & \widehat {ACB},IM \bot BC(gt),IN \bot AC(gt) \cr & \Rightarrow IM = IN \cr}\)
Từ (1) và (2) ta có IM = IN = IE.
b) Ta có \(IE \bot AB,IN \bot AC\) và IE = IN => I nằm trên tia phân giác của \(\widehat {BAC}\)
Vậy AI là tia phân giác của \(\widehat {BAC}.\)
