Bài 44. Cho tam giác ABC có.... Bài 44 trang 125 - Sách giáo khoa toán 7 tập 1 - Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (G.C.G)
Bài 44. Cho tam giác ABC có \(\widehat{ B}\)=\(\widehat{ C}\). Tia phân giác của góc A cắt BC tại D.
Chứng minh rằng.
a) ∆ADB=∆ADC.
b) AB=AC.

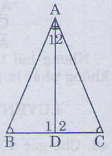
a) ∆ADB và ∆ ACD có:
Advertisements (Quảng cáo)
\(\widehat{ B}\)=\(\widehat{ C}\)(gt) (1)
\(\widehat{ A_{1}}\)=\(\widehat{ A_{2}}\)(AD là tia phân giác)
Nên \(\widehat{ D_{1}}\)=\(\widehat{ D_{2}}\)
AD cạnh chung.
Do đó ∆ADB=∆ADC(g.c.g)
b) ∆ADB=∆ADC(câu a)
Suy ra AB=AC .
