Bài 38. Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng AB=CD,AC=BD.. Bài 38 trang 124 - Sách giáo khoa toán 7 tập 1 - Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (G.C.G)
Bài 38. Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng
AB=CD,AC=BD.
Giải.
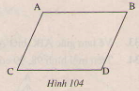
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
Advertisements (Quảng cáo)
\(\widehat{A_{1}}\)= \(\widehat{D_{1}}\)(so le trong AB//CD)
AD là cạnh chung.
\(\widehat{A_{2}}\)=\(\widehat{D_{2}}\)(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
