Advertisements (Quảng cáo)
Bài 6. Tìm các số đo \(x\) ở các hình sau:
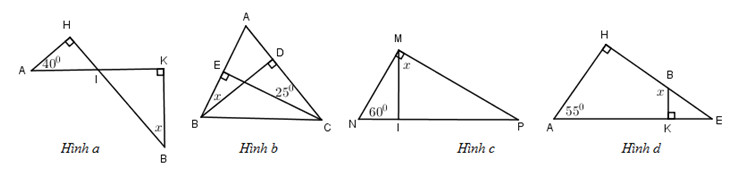
Hình a)
Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta có:
\(\widehat{A}+\widehat{AIH}\)= 900,
\(\widehat{B}\) + \(\widehat{BIK}\) = 900
mà \(\widehat{AIH}\)= \(\widehat{BIK}\) (vì hai góc đối đỉnh)
Suy ra \(\widehat{A}\) = \(\widehat{B}\)
Vậy \(\widehat{B}= 40^0\)
Hình b)
Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta có:
\(\widehat{ABD}\) +\(\widehat{A}= 90^0\), (1)
\(\widehat{ACE}\)+ \(\widehat{A}=90^0\), (2)
Từ (1) và (2) suy ra \(\widehat{ACE}\) = \(\widehat{ABD}=25^0\)
Advertisements (Quảng cáo)
Vậy \(x=25^0\)
Hình c)
Ta có: \(\widehat{NMI}\) + \(\widehat{PMI}= 90^0\),
\(\widehat{N }\) + \(\widehat{NMI}= 90^0\),
Suy ra \(\widehat{N }\) = \(\widehat{PMI}=60^0\)
Vậy \(x=60^0\)
Hình d)
Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta có:
\(\widehat{E }\) + \(\widehat{A}=90^0\)
\(\widehat{E }= 90^0- \widehat{A} = 90^0- 55^0= 35^0\)
\(\widehat{KBH }=\widehat{BKE}+ \widehat{E }\) (Góc ngoài tam giác \(BKE\))
\(= 90^0+ 35^0= 125^0\)
Vậy \(x=125^0\)