Bài 7. Cho tam giác \(ABC\) vuông tại \(A\). Kẻ \(AH\) vuông góc với \(BC\) (\(H\) nằm trên \(BC\)).
a) Tìm các cặp góc phụ nhau trong hình vẽ.
b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.

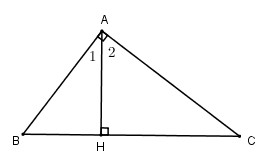
a) Tam giác \(ABC\) vuông tại \(A\) nên có \(\widehat{B }\) + \(\widehat{C }= 90^0\)
Hay \(\widehat{B }\), \(\widehat{C }\) phụ nhau,
Tam giác \(AHB\) vuông tại \(H\) nên có \(\widehat{B }\)+ \(\widehat{A_{1} }= 90^0\)
Hay \(\widehat{B }\), \(\widehat{A_{1} }\) phụ nhau.
Advertisements (Quảng cáo)
Tam giác \(AHC\) vuông tại \(H\) nên có \(\widehat{A_{2} }\)+ \(\widehat{C } = 90^0\)
hay \(\widehat{A_{2} }\), \(\widehat{C }\) phụ nhau.
b)
Ta có \(\widehat{B }\) + \(\widehat{C }= 90^0\)
\(\widehat{B }\)+ \(\widehat{A_{1} }= 90^0\)
\(\Rightarrow \widehat{A_{1} }=\widehat{C }\)
\(\widehat{B }\) + \(\widehat{C }=90^0\) và \(\widehat{A_{2} }\)+ \(\widehat{C }\) = \(90^0\)
\(\Rightarrow \widehat{A_{2} }\) = \(\widehat{B }\)
