Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) Hãy so sánh góc ADC và góc AEB.
b) Hãy so sánh các đoạn thẳng AD và AE.
Hướng dẫn làm bài:
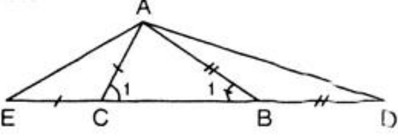
Trong ∆ABC, ta có AB > AC (gt) ⇒ \(\widehat {ACB} > \widehat {ABC}\) (1)
Từ (1) suy ra được: \(\widehat {AC{\rm{E}}} < \widehat {AB{\rm{D}}}\) (hai góc kề bù) (2)
- Trong tam giác cân ACE, ta có:
Advertisements (Quảng cáo)
\(\widehat {AC{\rm{E}}} = \widehat {E{\rm{A}}C}\) và \(\widehat {A{\rm{E}}C} + \widehat {E{\rm{A}}C} + \widehat {AC{\rm{E}}} = {180^0}\)
hay \(\widehat {AC{\rm{E}}} = 2\widehat {A{\rm{E}}C} = {180^0} \Rightarrow \widehat {A{\rm{E}}C} = {{{{180}^0} - \widehat {AC{\rm{E}}}} \over 2}\) (3)
- Tương tự, trong tam giác cân ABD, ta có:
\(\widehat {A{\rm{D}}B} = {{{{180}^0} - \widehat {AB{\rm{D}}}} \over 2}\) (4)
- Mà \(\widehat {AC{\rm{E}}} < \widehat {AB{\rm{D}}}\) (do (2))
Từ (2), (3), (4) suy ra: \({{{{180}^0} - \widehat {AC{\rm{E}}}} \over 2} > {{{{180}^0} - \widehat {AB{\rm{D}}}} \over 2}\)
suy ra \(\widehat {A{\rm{E}}C} > \widehat {A{\rm{D}}B}\) hay \(\widehat {A{\rm{E}}B} > \widehat {A{\rm{D}}C}\) (đpcm)
b) Xét ∆AED, ta có: \(\widehat {A{\rm{E}}B} > \widehat {A{\rm{D}}C}\) . Suy ra AD > AE
