
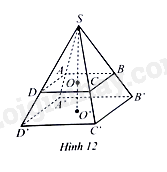
Cho hai hình chóp tứ giác đều \(S.ABCD\) và \(S.A’B’C’D’\) lần lượt có chiều cao \(SO\) và \(SO’\). Biết \(AB = 2a,A’B’ = 3a,SO = 2b,SO’ = 3b\) (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều \(S.ABCD\) và \(S.A’B’C’D’\) biết rẳng \(a\) và \(b\) cùng đơn vị đo.

Áp dụng công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\), trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều. Sau đó tính tỉ số thể tích của hai hình chóp tứ giác đều đó.

Advertisements (Quảng cáo)
Thể tích của hình chóp tứ giác đều \(S.ABCD\) là:
\(\frac{1}{3}.\left( {2a.2a} \right).2b = \frac{{8{a^2}b}}{3}\) (đơn vị thể tích)
Thể tích của hình chóp tứ giác đều \(S.A’B’C’D’\) là:
\(\frac{1}{3}.\left( {3a.3a} \right).3b = 9{a^2}b\) (đơn vị thể tích)
Tỉ số thể tích của hình chóp tứ giác đều \(S.ABCD\) và \(S.A’B’C’D’\) là:
\(\frac{{8{a^2}b}}{3}:\left( {9{a^2}b} \right) = \frac{8}{{27}}\)
