Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao?
Giải:
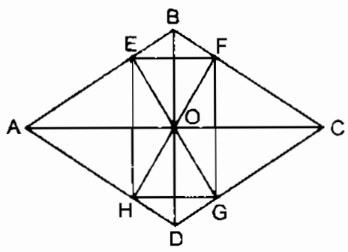
Ta có: AB // CD (gt)
OE ⊥ AB (gt)
⇒ OE ⊥ CD
OG ⊥ CD (gt)
Suy ra: OE trùng với OG nên ba điểm O, E, G thẳng hàng.
BC // AD (gt)
OF ⊥ BC (gt)
Advertisements (Quảng cáo)
⇒ OF ⊥ AD
OH ⊥ AD (gt)
Suy ra : OF trùng với OH nên ba điểm O, H, F thẳng hàng
AC và BD là đường phân giác các góc của hình thoi
OE = OF (tính chất tia phân giác) (1)
OE = OH (tính chất tia phân giác) (2)
OH = OG (tính chất tia phân giác) (3)
Từ (1), (2) và (3) suy ra: OE = OF = OH = OG
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên là hình chữ nhật.
