Chứng minh rằng tứ giác AMDN là hình vuông.. Câu 144 trang 98 Sách bài tập (SBT) Toán 8 tập 1 – Bài 12. Hình vuông
Advertisements (Quảng cáo)
Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
Giải:
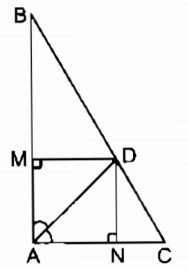
Xét tứ giác AMDN:
\(\widehat {MAN} = \)1v (gt)
DM ⊥ AB (gt)
\( \Rightarrow \widehat {AMD}\)= 1v
Advertisements (Quảng cáo)
DN ⊥ AC (gt)
\( \Rightarrow \widehat {AND}\)=1v
Suy ra: Tứ giác AMDN là hình chữ nhật (vì có ba góc vuông), có đường chéo AD là đường phân giác của góc A.
Vậy : Hình chữ nhật AMDN là hình vuông.
Mục lục môn Toán 8 (SBT)