Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
Giải:
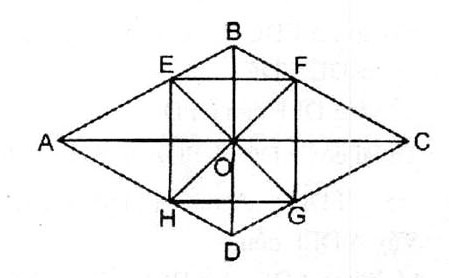
Ta có: \(\widehat {AOB}\)và \)\widehat {COD}\) đối đỉnh nên E, O, G thẳng hàng
\(\widehat {BOC}\)và \(\widehat {AOD}\) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
\(\widehat {EBO} = \widehat {FBO}\) (tính chất hình thoi)
OB cạnh chung
\(\widehat {EOB} = \widehat {FOB} = {45^0}\) (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
\(\widehat {EBO} = \widehat {GDO}\) (so le trong)
OB = OD(tính chất hình thoi)
Advertisements (Quảng cáo)
\(\widehat {EOB} = \widehat {GOD}\) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
\(\widehat {EAO} = \widehat {HAO}\) (tính chất hình thoi)
OA cạnh chung
\(\widehat {EOA} = \widehat {HOA} = {45^0}\) (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
