Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho\(\widehat {FAD} = \widehat {FDA} = {15^0}\).
a. Vẽ điểm F trong hình vuông sao cho\(\widehat {FAD} = \widehat {FDA} = {15^0}\). Chứng minh rằng tam giác DEF là tam giác đều.
b. Chứng minh rằng tam giác ABE là tam giác đều.
Giải:
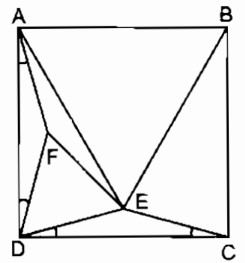
a. Xét ∆ EDC và ∆ FDA :
\(\widehat {EDC} = \widehat {FAD} = {15^0}\)
DC = AD (gt)
\(\widehat {ECD} = \widehat {FDA} = {15^0}\)
Do đó: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Ta lại có:
\(\eqalign{ & \widehat {ADC} = \widehat {FDA} + \widehat {FDE} + \widehat {EDC} \cr & \Rightarrow \widehat {FDE} = \widehat {ADC} - \left( {\widehat {FDA} + \widehat {EDC}} \right) \cr & = {90^0} - \left( {{{15}^0} + {{15}^0}} \right) = {60^0} \cr} \)
Vậy ∆ DEF đều.
b. Xét ∆ ADE và ∆ BCE:
Advertisements (Quảng cáo)
ED = EC (vì ∆ EDC cân tại E)
\(\widehat {ADE} = \widehat {BCE} = {75^0}\)
AD = BC (gt)
Do đó: ∆ ADE = ∆ BCE (c.g.c)
⇒ AE = BE (1)
Trong ∆ AFD ta có:
\(\eqalign{ & \widehat {AFD} = {180^0} - \left( {\widehat {FAD} + \widehat {FDA}} \right) \cr & = {180^0} - \left( {{{15}^0} + {{15}^0}} \right) = {150^0} \cr & \widehat {AFD} + \widehat {DFE} + \widehat {AFE} = {360^0} \cr & \Rightarrow \widehat {AFE} = {360^0} - \left( {\widehat {AFD} + \widehat {DFE}} \right) \cr & = {360^0} - \left( {{{150}^0} + {{60}^0}} \right) = {150^0} \cr} \)
Xét ∆ AFD và ∆ AEF:
AF cạnh chung
\(\widehat {AFD} = \widehat {AFE} = {150^0}\)
DF = EF (vì ∆ DFE đều)
Do đó: ∆ AFD = ∆ AEF (c.g.c)
⇒ AE = AD
AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE. Vậy ∆ AEB đều.
