a. Chứng minh rằng EC = BH, EC ⊥ BH.. Câu 153 trang 99 Sách bài tập (SBT) Toán 8 tập 1 - Bài 12. Hình vuông
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.
a. Chứng minh rằng EC = BH, EC ⊥ BH.
b. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?
Giải:
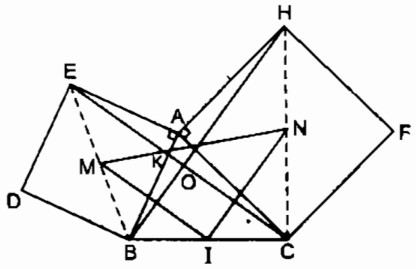
a. Ta có: \(\widehat {BAH} = \widehat {BAC} + \widehat {CAH} = \widehat {BAC} + {90^0}\)
\(\widehat {EAC} = \widehat {BAC} + \widehat {BAE} = \widehat {BAC} + {90^0}\)
Suy ra: \(\widehat {BAH} = \widehat {EAC}\)
- Xét ∆ BAH và ∆ EAC:
BA = EA (vì ABDE là hình vuông)
\(\widehat {BAH} = \widehat {EAC}\) (chứng minh trên)
AH = AC (vì ACFH là hình vuông)
Do đó: ∆ BAH = ∆ EAC (c.g.c)
⇒ BH = EC
Gọi giao điểm của EC với AB và BH lần lượt là K và O.
\(\widehat {AEC} = \widehat {ABH}\) (vì ∆ BAH = ∆ EAC) (1)
hay \(\widehat {AEK} = \widehat {OBK}\)
- Trong ∆ AEK ta có: \(\widehat {EAK} = {90^0}\)
\( \Rightarrow \widehat {AEK} + \widehat {AKE} = {90^0}\) (2)
\(\widehat {AKE} = \widehat {OKB}\) (đối đỉnh) (3)
Từ (1) và (2) suy ra: \(\widehat {OKB} + \widehat {OBK} = {90^0}\)
Advertisements (Quảng cáo)
- Trong ∆ BOK ta có: \(\widehat {BOK} + \widehat {OKB} + \widehat {OBK} = {180^0}\)
\( \Rightarrow \widehat {BOK} = {180^0} - \left( {\widehat {OKB} + \widehat {OBK}} \right) = {180^0} - {90^0} = {90^0}\)
Suy ra: EC ⊥ BH
b. Trong ∆ EBC ta có:
M là trung điểm của EB (tính chất hình vuông)
I là trung điểm của BC (gt)
nên MI là đường trung bình của tam giác EBC
⇒ MI = \({1 \over 2}\)EC và MI // EC (tính chất đường trung bình của tam giác)
- Trong ∆ BCH ta có:
I là trung điểm của BC (gt)
N là trung điểm của CH (tính chất hình vuông)
nên NI là đường trung bình của ∆ BCH
⇒ NI = \({1 \over 2}\)BH và NI // BH (tính chất đường trung bình của tam giác)
BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH
NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay \(\widehat {MIN} = {90^0}\)
Vậy ∆ IMN vuông cân tại I.
