a. Chứng minh rằng CE vuông góc với DF. Câu 155 trang 99 Sách bài tập (SBT) Toán 8 tập 1 - Bài 12. Hình vuông
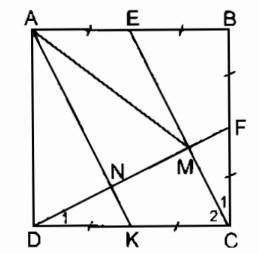
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC.
a. Chứng minh rằng CE vuông góc với DF
b. Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AD
HD . Gọi K là trung điểm của CD. Chứng minh rằng KA // CE.

a. Xét ∆ BEC và ∆ CFD:
BE = CF (gt)
\(\widehat B = \widehat C = {90^0}\)
BC = CD (gt)
Do đó: ∆ BEC = ∆ CFD (c.g.c)
\(\eqalign{ & \Rightarrow {\widehat C_1} = {\widehat D_1} \cr & {\widehat C_1} + {\widehat C_2} = {90^0} \cr} \)
Suy ra: \({\widehat D_1} + {\widehat C_2} = {90^0}\)
Trong ∆ DCM có \({\widehat D_1} + {\widehat C_2} = {90^0}\)
Advertisements (Quảng cáo)
Suy ra: \(\widehat {DMC} = {90^0}\). Vậy CE ⊥ DF
b. Gọi K là trung điểm của DC, AK cắt DF tại N.
Xét tứ giác AKCE ta có:
AB // CD hay AE // CK
AE = \({1 \over 2}\)AB (gt)
CK = \({1 \over 2}\)CD (theo cách vẽ)
Suy ra: AE // CK nên tứ giác AKCE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
AK // CE
DF ⊥ CE (chứng minh trên)⇒ AK ⊥ DF hay AN ⊥ DM
Trong ∆ DMC ta có: DK = KC
KN // CM
nên DN = MN (tính chất đường trung bình của tam giác)
Suy ra: ∆ ADM cân tại A (vì có đường cao vừa là đường trung tuyến)
⇒ AD = AM
