Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD.
a. Tính khoảng cách từ I đến AB
b. Khi điểm M di chuyển trên đoạn thẳng AB thì điểm I di chuyển trên đường nào ?
Giải:
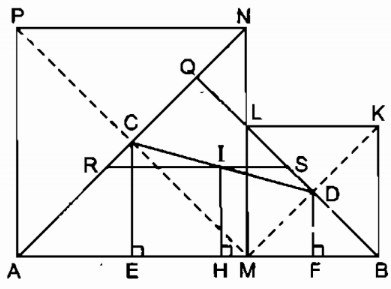
a. Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
⇒ CE // DF // IH
IC = ID (gt)
nên IH là đường trung bình của hình thang DCEF
\( \Rightarrow IH = {{DF + CE} \over 2}\) (1)
C là tâm hình vuông AMNP
⇒ ∆ CAM là tam giác vuông cân tại C
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = \({1 \over 2}\)AM
Advertisements (Quảng cáo)
D là tâm hình vuông BMLK ⇒ ∆ DBM vuông cân tại D
DF ⊥ BM
⇒ DF là đường trung tuyến (tính chất tam giác cân) ⇒ DF = \({1 \over 2}\)BM
Vậy CE + DF = \({1 \over 2}\)AM + \({1 \over 2}\)BM = \({1 \over 2}\) (AM + BM) = \({1 \over 2}\)AB = \({a \over 2}\) ⇒ IH = \({{{a \over 2}} \over 2} = {a \over 4}\)
b. Gọi Q là giao điểm của BL và AN
Ta có: AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hai góc kề bù)
Suy ra: BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng \({a \over 4}\) nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng \({a \over 4}\)
Khi M trùng B thì I trùng với S là trung điểm của BQ
Khi M trùng với A thì I trùng với R là trung điểm của AQ
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng \({a \over 4}\) .
