Chứng minh rằng. Câu 18 trang 87 Sách bài tập (SBT) Toán 8 tập 2 - Bài 3. Tính chất đường phân giác của tam giác
Tam giác ABC có các đường phân giác AD, BE và CF
Chứng minh rằng:
\({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = 1\)
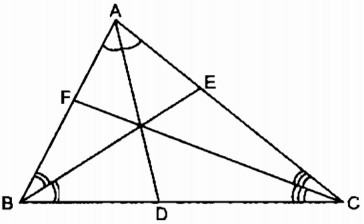
Trong tam giác ABC, ta có: AD là đường phân giác của \(\widehat {BAC}\)
Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác ) (1)
Advertisements (Quảng cáo)
BE là đường phân giác \(\widehat {ABC}\)
Suy ra: \({{EC} \over {EA}} = {{BC} \over {AB}}\) (tính chất đường phân giác ) (2)
CF là đường phân giác của \(\widehat {ACB}\)
Suy ra: \({{FA} \over {FB}} = {{CA} \over {CB}}\) (tính chất đường phân giác ) (3)
Nhân từng vế (1), (2) và (3), ta có:
\({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = {{AB} \over {AC}}.{{BC} \over {AB}}.{{CA} \over {CB}} = 1\)