Cho ba đoạn thẳng AB = 3cm, CD = 5cm, EF = 2cm. Dựng đoạn thẳng thứ tư có độ dài a sao cho \({{AB} \over {CD}} = {{EF} \over a}\) hay \({3 \over 5} = {2 \over a}\) . Tính giá trị của a.
Giải:
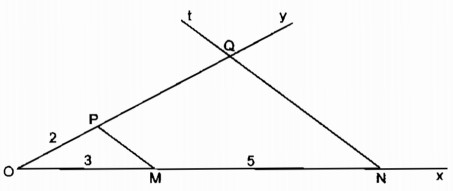
Cách dựng:
- Dựng hai tia chung gốc Ox và Oy phân biệt không đối nhau.
- Trên Ox dựng đoạn OM = AM = 3cm và dựng đoạn MN = CD = 5cm sao cho M nằm giữa O và N.
- Trên đoạn Oy dựng đoạn OP = EF = 2cm.
- Dựng đường thẳng PM
Advertisements (Quảng cáo)
- Từ N dựng đường thẳng song song với PM cắt tia Oy tại Q. Đoạn thẳng PQ = a cần dựng.
Chứng minh:
Theo cách dựng, ta có: PM // NQ
Trong ∆ ONQ ta có: PM // NQ
Suy ra: \({{OM} \over {MN}} = {{OP} \over {PQ}}\) (Định lí Ta-lét )
Suy ra: \({{AB} \over {CD}} = {{EF} \over a}\) hay \({3 \over 5} = {2 \over a}\)
Vậy \(a = {{10} \over 3}\) (cm).
